Ways of protecting your private data – a short intro to cryptography
Encryption is important. Although intuitively you might say that you have nothing to hide, it’s important to ask yourself the following question: would you be willing to give your Facebook password to a stranger or publish it online? Probably not. Most people have something to hide and encryption is one way of safe-guarding your private information.
The focus of this article is on how to protect your data against physical compromise (symmetric encryption), when you send it to someone (asymmetric encryption) and when you would like it to be retrievable (secret sharing).
Your own data (symmetric encryption)
If you want to protect files that only you will be working with, symmetric encryption is quite useful. Symmetric encryption means there is only one key to encrypt and decrypt data.
By default, it’s a good idea to have full-disk encryption to make sure your files are inaccessible if the computer or phone is lost. If you have a USB stick, it’s also useful to encrypt the information on it as these tend to be lost more frequently.
Tech savvy:
Nowadays, AES (Rijndael) is the one that is considered to be secure, so by default this is the way to go. The most common AES versions are with 128-bit keys and 256-bit keys. For most cases, 128-bit keys should be ok, but for extra paranoid users, you can both increase the key size and combine it with other encryption methods, such as AES-Twofish-Serpent (all of these are AES finalists).
If you leave your computer unattended, please make sure it’s turned off. Preferably you should let it be off in 10 min to avoid cold-boot attack.
Tools
- BitLocker (built into Windows, mainly for full-disk encryption)
- VeraCrypt (cross platform, full-disk encryption and encrypted containers)
Sharing data with others (asymmetric encryption)
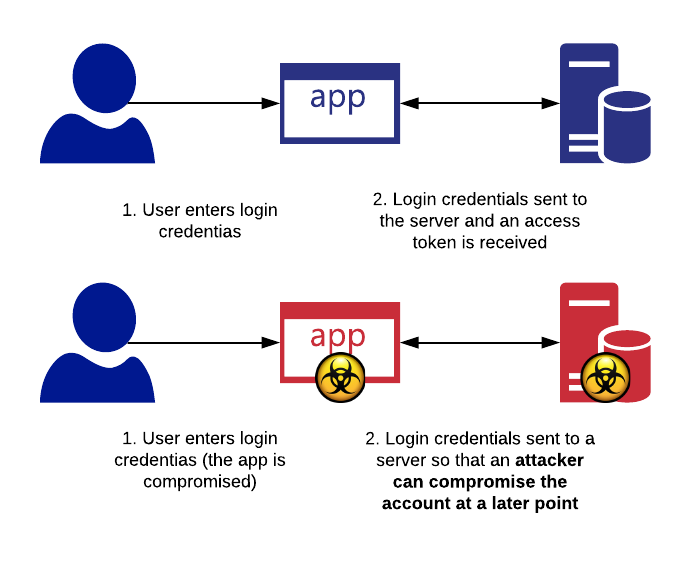
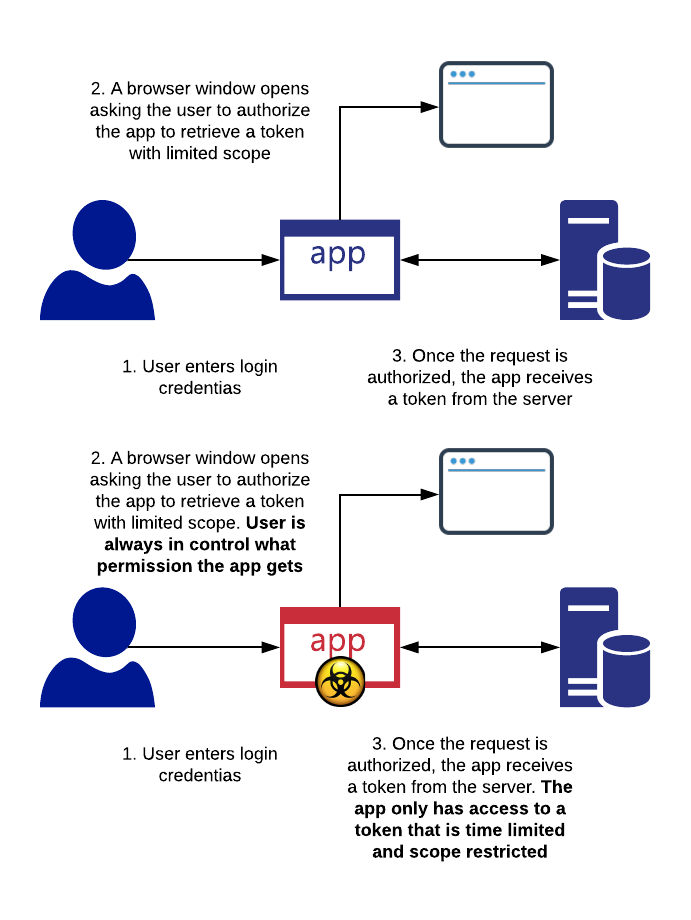
Imagine you would like to allow everyone to contact you securely without having to agree on a secret key first (which is the case with symmetric encryption). This is where asymmetric encryption is useful. Instead of one secret key there are two: one to encrypt and one to decrypt.
There is a good analogy with real objects. To enable others to send you shipments securely, one way of accomplishing this would be to hand out unlocked padlocks with a box. If they want to send you something, they would lock the box with your padlock, ensuring that only you can open it.
Tech savvy:
The most common asymmetric encryption methods are RSA and Elliptic curves. There are some arguments which method is more secure. Both RSA and ECC base their security on mathematical problems that are hard to solve. Since we are better at factoring large numbers (which can help to break RSA) than we are at solving the elliptic curve discrete logarithm problem, RSA keys tend to be larger than those in ECC (2048 vs 256) to guarantee the same level of security.
There are also different kinds of ECC curves, ones proposed by NSA (NIST curves) and by independent researches, eg Curve25519 by Daniel J. Bernstein, and there are mixed opinions on which one to choose (an interesting article on the topic).
I tend to use either RSA 4096 or Curve25519 for ECC.
Tools
Splitting a secret (secret sharing)
In case something happens to you and you don’t want your encrypted data to be inaccessible, you can break up a password (eg to your personal files) into multiple pieces that you give to your close friends. All friends need to agree to retrieve the original secret.
Tech savvy:
Additive secret sharing (code snippet shown later) is the easiest to understand and implement but it requires all parties to be present to retrieve the secret. Shamir Secret sharing allows us to define how many shares will be necessary to get the secret.
The cool thing about secret sharing is that it’s unconditionally secure, meaning that we need all shares to retrieve the secret and we don’t gain more info with more shares. It also means that the modulus Q does not need to be large.
If it’s ok to require all parties to be present to get the secret key, you can use the code for additive secret sharing below. Your secret can be any number less than 2^512 (512 bits).
import secrets
Q = 2**512
def encrypt(x, no_shares = 3):
"""
Splits the secret up into 'no_shares' shares
"""
shares = [secrets.randbelow(Q+1) for i in range(no_shares - 1)]
shares.append((x - sum(shares)) % Q)
return shares
def decrypt(shares):
"""
Combine all shares to retrieve the secret
"""
return sum(shares) % QTools
- Additive secret sharing (the code above)
- Shamir Secret Sharing (Python)